もちろんトレードの結果は完全に想定通りにはならない
以前、損益の期待値はyを損益、xを取引回数とすると、aを定数としてy=axの式で表せると書きましたが、数学的により正確にはyは実現値ではなく期待値(予測値)なので、yに^(ハット)を付けて
![]()
と表します。しかし、これはあくまで想定なので、実際の結果はかならずしもこの通りにはなりません。違う値になることも多いです。この想定の値と実際の値の違いを「残差」といいます。
ここで実際の運用結果(実現値)の損益をあらためてy、勝ち負けの回数の残差をe(一般的に残差はeで表されます)とすると、残差eがプラス(勝ちの回数が予想よりも多い)場合は、予想よりもe回分、TP(利食い)が増えSL(損切り:ストップロス)が減るので
![]()
となり、残差eがマイナス(負けの回数が予想よりも多い)の場合は、予想よりもe回分、TP(利食い)が減りSL(損切り:ストップロス)が増えるので
![]()
となります。この式からも分かるように、x(取引回数)の値が十分に大きく、勝ち負けの回数が正規分布に従って分散するとしても、y(損益)の値はTPおよびSLの値の影響を受けます。TPやSLの値があまりに大きい場合は、a(期待値)の値が多少高くても、y(損益)の値は容易にマイナスとなってしまうのです。また、もしTPとSLの値に大きく差がある場合は、y(損益)の分散は正規分布とは全く違うものになってしまいます。
具体例を挙げてみる
例えばTP(利食い)とSL(ストップロス:損切り)が同じ1,000円で、勝率が70%のバックテストが得られたEAがあるとします。
1回の勝ちで得られる利益(または損失)が1,000円の場合は、100回の取引で得られる期待値は、以下の通りになります
■勝率70% 想定通りの結果
もし、これが想定通りの勝ち負けの割合になった場合は
勝ち70回 : 負け30回
なので
(勝ち:1,000円 × 70回) – (負け:-1,000円 × 30回) =損益: +40,000円
となります。これを上記の式に当てはめると、yを損益40,000、xを取引回数100として
y=400x
となり、1回の取引の期待値は400円となります。
しかし、これはあくまで想定なので、実際の結果はかならずしもこの通りにはなりません。勝ちと負けの比は7:3ではなく、違う値になることも多いです。
■勝率70% 残差-10回の結果
上の例で、もし10回分、想定負けが多くなった場合は(残差 = -10回)の場合、実際の利益は
(勝ち:1,000円 × 60回) – (負け:1,000円 × 40回) = 損益:+20,000円
となります。これを上記の式にあてはめ、yを損益20,000、xを取引回数100、残差をeを10として書くと
y=400x – TP × e – SL × e
=400 × 100 – 1,000×10 – 1,000×10
=40,000 – 20,000
=20,000
となります。
TPやSLが大きすぎるとシステムが容易に破綻する
ここでありがちなのが、初心者のトレーダーはとにかく負けを嫌がるので、例えばTL:1,000円、SL:10,000円とSLの値だけ10倍に高くして、勝率99%を実現するケースです。その場合はの残差による影響はどうなるでしょうか。
■勝率99% 想定通りの結果
勝ち99回 : 負け1回
なので、想定通りの結果がでた場合は
(勝ち:1,000円 × 99回) – (負け:10,000円 × 1回) = 損益:+89,000円
となり想定通りであれば、さきほどより利益は多くなります。これを上記の式に当てはめると、yを損益89,000、xを取引回数100として
y=890x
となり、1回の取引の期待値は890円となります。この期待値はさきほどの期待値400円より大きいです。
■勝率99% 残差-10回の結果
しかし、さきほどと同じ残差が発生した場合は
(勝ち:1,000円 × 89回) – (負け:10,000円 × 11回) = 損益:-21,000円
となり、赤字となってしまします。これを先ほどと同じ式にあてはめて書くと
y=890x – TP × e – SL × e
=890 × 100 – 1,000×10 – 1,0000×10
=89,000 – 110,000
=-21,000
となります。
たとえ、10回未満の残差であっても、TPやSLの値が大きい場合は、少ない回数の残差であっという間に収益が悪化してしまうのです。
ちなにこの場合は、勝ちの回数は最大100回なので、勝ち方向への残差は最大+1回なので、負け方向の残差の最大値ばかり大きくなってしまいます。このように、二項分布において確率があまりに高い場合は、勝ち方向への残差の上限が制限されるにもかかわらず、負け方向の残差は無限に広がってしまします。このような現象を統計学の世界ではポアソン分布と言いますが、ここでは詳しく説明しません。
ただし、実際には勝率70%の場合に比べて、勝率99%の場合は、10回の残差が発生する確率自体は低くなります。これについては別の記事で説明しようと思います。
システムトレードにおいて最も重要なのは生き残ること
システムトレードにおいて最も重要なのは生き残ることであり、トータルの運用結果がマイナスとなるのは致命的のため最も避けなければなりません。口座が破綻しなければ次のチャンスがまだありますが、虎の子の口座が破綻してしまっては次の勝負をすることはもはやできないからです(たとえ余剰資産で運用したとしても、心理的ダメージは計り知れないものがあります)。
TPやSL(損切り:ストップロス)の値を極端に大きくし、それに依存した期待値とすることは、トレーディングシステムを破綻させる可能性を高めてしまうのです。

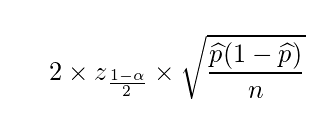

コメント